10.1- Un triciclo con ruedas cuadradas
Este triciclo no puede rodar sobre una carretera plana. Pero avanza sin problemas sobre un “camino” hecho de superficies curvas en forma de… catenarias invertidas.
La ecuación de esta curva estuvo encontrada por Jean Bernoulli, Huygens y Leibniz 1691.
Ilustración: arcos en forma de chainette invertidos realizadas por el arquitecto Gaudy para la Sagrada Familia en Barcelona.
Idea: Tokai Universidad - Realización: Centre•Sciences
10.2- El flipper del azar
Este flipper consiste en un tablero inclinado, que tiene en su extremo superior un depósito para guardar bolas.
Tiene una configuración triangular de clavos colocados a intervalos iguales a lo largo de líneas horizontales (en la primera uno, dos en la segunda,…) y que tiene cajones individuales en el extremo inferior para recoger las bolas.
Este instrumento, llamado aparato de Galton, permite hacer visibles numerosas propiedades de la teoría de la probabilidad.
Fue Francis Galton quien demostró en 1889 esta ley de distribución probabilística llamada distribución binomial. Encontramos el triángulo de números llamado triángulo de Pascual.
Idea: Tokai Universidad - Realización: Centre•Sciences
10.3- Un árbol musical
¿Conoce esta canción, tan conocida por los niños y… los pianistas debutantes?
¿Dónde están las matemáticas?
Las teclas de un xilófono producen diferentes sonidos dependiendo de su longitud y de la densidad del material que las forma.
Este árbol musical es una adaptación matemática y artística del xilófono.
Cada rama del árbol representa una tecla del xilófono. Las teclas se sitúan de manera que la bola descienda de rama en rama, tocando cada tecla para dar lugar a una serie de notas musicales que producen una cierta melodía.
Algunas ramas están recubiertas por fieltro para indicar un silencio: no se produce ningún sonido cuando la bola choca contra ellas.
Idea: Tokai Universidad – Realización: Centre•Sciences
10.4- ¿Qué ve?
Este bloque de madera puede verse como la silueta de un animal… o ¡de otro!
Utilizada en tests psicológicos, esta escultura muestra que en matemáticas, como en la vida, hay que ser “flexibles” y abordar los problemas bajo todos los ángulos.
Idea: Tokai Universidad - Realización: Centre•Sciences
10.5- La Espiral Logarítmica
Haga girar el disco…¿qué ve?
La espiral logarítmica se encuentra a menudo en la naturaleza. Como muestran las conchas de los caracoles o los nautilus, las espirales de la naturaleza conservan la misma forma a lo largo de todo su crecimiento.
Una espiral logarítmica se puede trazar utilizando un círculo que gira, como se muestra en la imagen. Puede expandirse o contraerse hasta el infinito.
En un sistema de coordenadas polares, la espiral logarítmica tiene por ecuación R = a. rθ, donde a y r son constantes.
Cuando el ángulo θ aumenta en α unidades, R aumenta proporcionalmente a rα.
Así, haciendo girar esta espiral logarítmica en un sentido u otro, verá aparecer una espiral que se dilata o se contrae.
Idea: Tokai Uversidad - Realización: Centre•Sciences
10.6- Seis Pirámides para Una Torre
Con estos 6 bloques, intente construir una gran torre.
Si lo consigue, entonces podrá encontrar el volumen de cada pirámide.
Cada una de ellas es la suma de estos cuadrados: 12 + 22 + 32 + 42 +.......+ 82!
Estos bloques permiten dar una demostració de la fórmula:
de k = 1 a n, ∑ k2 = n(n+1)(2n+1)/6
El mismo procedimiento utilizado para n = 8 se puede aplicar para cualquier n.
La torre final, de dimensiones n, n+1, 2n+1, combina 6 pirámides.
Así: 6(12 +22 +32 + ... +n2) = n x (n+1) x (2n+1) y se obtiene la fórmula.
Esta construcción se debe al matemático chino, Yang Hui, en el siglo XIII.
Idea: Tokai Uversidad - Realización: Centre•Sciences
10.7- ¿Qué es una Cicloide?
Roll the disk along the frame and observe the curve traced by one white point.
A cycloid is a curve traced by a fixed point on the circumference of the circle as the circle rotates along a straight line. Idea: Tokai University – Realización: Centre•Sciences
10.8- La cinta de Möbius
¿Cuántas caras, cuántos bordes tiene esta cinta, dice cinta de Möbius?
¿ Puede citar objetos que tienen una sola cara y un cero borde?
¿ Dos caras y un solo borde? ¿ Dos bordes y dos caras?
Realice una cinta de Möbius con una banda de papel y recorte esta cinta por el medio de la banda. ¿ Cuántas cintas va a obtener? ¿ Cuántas caras y cuántos bordes?
Idea: Ferdinand Möbius (1790-1868) - Realización: A partir de una obra de M.C. Escher (1898-1972)
10.9- Papiroflexia y Fractal
¿Cómo hacer esto?
Tomar un rectángulo de papel 1 x 2, ceda en dos, corte en dos según el pliegue, despliegue y marcar los dos valles para obtener el 1r cubo. Repetir la misma secuencia sobre, cada cuadrado gris: dibujar, cortar, desplegar, y doblar las montañas. Y empiece de nuevo …
Primero, el más grande, está en el centro. Luego usted añade dos más pequeño. Si usted sube a esta pequeña escalera, usted encuentra los cubos en esta orden: 2-1-2.
Mirando este modelo desde arriba, se puede dar un valor a los pliegue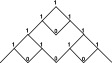s.
0 para los pliegues en montaña y 1 para los valles. Se obtendrá un triángulo codificado que usted puede comparar con triángulo de Pascal módulo 2.
Idea y realización: Jean Brette (Paris)
10.10- Coloque 11 Cubos en la Maleta
¿Cuántos cubos de lado la unidad pueden meterse en una maleta cuadrada de lado 39 cm?
A menudo nos enfrentamos con este problema de meter pequeños paquetes en un contenedor mayor.
Es evidente que se pueden meter 9 cubos en esta maleta. Incluso es posible hacerlo con 10 cubos.
Pero con 11, ¡hay que encontrar la disposición adecuada!
Este problema ilustra uno más general: ¿cuál es el menor cuadrado en el que se pueden colocar n cubos de lado una unidad?
Para 11 cubos, la menor maleta cuadrada conocida tiene por lado 38,77 cm. Hecho descubierto por W. Trump.
Si n = m2, entonces la menor maleta cuadrada en la que se pueden meter n cubos tiene por lado m.
Si n no es un cuadrado perfecto, el problema permanece abierto.
Idea: Tokai University – Realización: Centre•Sciences
10.11– Péndulo caótico
Lance péndulo y trate de adivinar por encima de cual imán va a pararse.
Si péndulo se va de un punto azul, se parará sobre el imán azul. Pero cerca de las fronteras, cualquier pequeña divergencia modifica completamente la trayectoria de péndulo.
Decimos que el sistema es caótico.
El efecto célebre mariposa: el vuelo de una mariposa en Brasil podría causar un tornado en Texas varias semanas más tarde, es una metáfora presentada por Edward Lorenz en 1963 para ilustrar el hecho de que los sistemas meteorológicos son caóticos.
Idea y realización: Centre•Sciences